I am associate professor at
Université
Grenoble Alpes
Grenoble,
France.
My research activity is focused on
computational geophysics at ISTerre
lab
I teach courses related to geophysics in the PHITEM
department of (Physics, Mechanical Engineering,
Planetary and Earth Sciences department)
|
email : romain.brossier_at_univ-grenoble-alpes.fr
Physical address:
Mail
address: CS 40700 |
LINK
TO PUBLICATIONS LIST AND PDFs
LINK
TO PROCEEDINGS LIST AND PDFs
LINK TO
BOOK CHAPTER LIST AND PDFs
LINK
TO THESIS LIST AND PDFs
Link
to my Google Scholar Page
My
research activity is focused on high resolution quantitative imaging
of the Earth at various scales. I'm leading the SEISCOPE
II research project focused on developement and application of
original imaging techniques.
I have collaborated, for more than
10 years, with people from (alphabetic order) : 3SR, BRGM,
BULL-ATOS, EDF, GIPSA-Lab, IFSTTAR, INTEL, INRIA, IRIT/INRIA/ENSEEIHT
(MUMPS team), IRSN, JAMSTEC, NVIDIA, SAUDI ARAMCO, TOTAL...
I mainly use the full waveform inversion method to perform
quantitative imaging of Earth from seismic data, but also
electromagnetic data.
Full Waveform Inversion (FWI) is an
appealing method to obtain high resolution quantitative images of
Earth physical properties, but require to deal with challenging
numerical and physical issues. My work is focused on development of
methodologies and applications of FWI in the time (and previously in
frequency domain), leading to different research topics :
Numerical methods for PDE : I work with various methods to solve the acoustic and elastic wave-equations with various approximations (acoustic/ elastic/ isotropic/ anisotropic/ electromagnetic). Right now, I mainly use Finite Differences for acoustic media and Finite Elements methods (spectral element) for elastic media.
This part is the core of the forward problem of the FWI.
The
discretized formulation in the frequency domain leads to the
resolution of huge sparse linear systems. These systems are
efficiently solved using the mutifrontal parallel solver MUMPS.
In the past, the triangular meshes used for FE DG method has
been built with Triangle.
In the time domain, usual time-stepping is used. Bellow are
image and small movie of what can be done with our modeling and
inversion code SEM46 (this code is available for SEISCOPE sponsors
and collaborators)
|
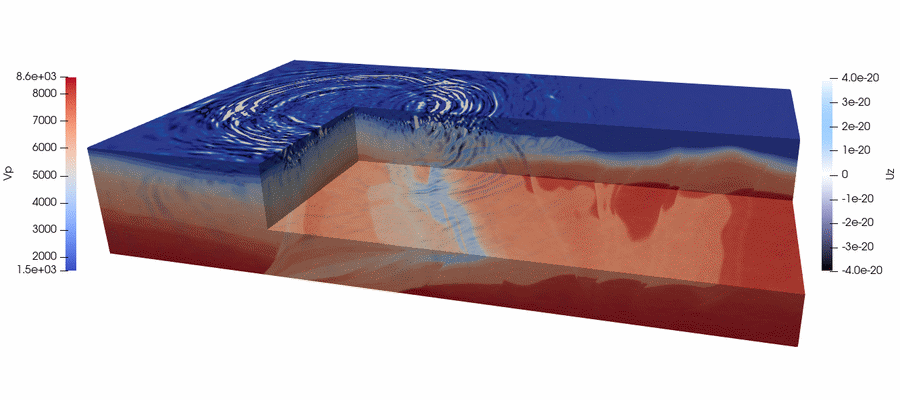
Large-scale Optimization problems : FWI is a linearized iterative process with many unknowns. I am interested in using efficient (in computational time and memory) optimization algorithms to solve the FWI problem. We have intensely used preconditioned Conjugate Gradient and L-BFGS. We developed truncated-Newton methods to improve the hessian information used in the inversion.
You can find our Open-Source optimization toolbox (developed by Ludovic Métivier) here
Non-linear inverse problems : FWI is a highly non-linear inverse problem, particularly in complex environments that produce complex data... I am interested in developing multi-scale/multi-step/hierarchical procedures to mitigate the non-linearity of the inverse problem, in order to converge to the global minimum. Strategies related to the physics and applied mathematics are investigated.
Multi-parameters inversion : Considering the acoustic or elastic-wave equation for propagation, physical parameters like wave velocities, density, attenuation,... can be reconstructed during the FWI procedure. Depending on the environment and medium, data can be affected by different signature weights of the parameters. I am interested in developing hierarchical inversion procedure to image the different parameter classes.
Robust inversion formalisms : FWI is classically develop under a least-square formalism. However, alternatives to least-squares exist and could present more robust behaviors… We particularly worked on Optimal Transports approach for several years.
Various scales applications : FWI can be applied to data at various scales from near-surface geotechnic and civil engineering problems to Oil&Gaz industry exploration scales, to crustal imaging,.... and one day maybe, to the global scale. I work mainly for lab-scale, ocean acoustics, near-surface, exploration scales and regional scales.
High performance parallel computing : FWI is a computationaly intensive method that requires efficient implementations of both forward and inverse problems for parallel executions on high performances computing centers with distributed-memory architectures. I mainly work on the CIMENT center at Observatoire des Sciences de l'Univers de Grenoble and the CINES, TGCC and IDRIS national centers. I also massively used the SIGAMM mesocenter at Observatoire de la Côte d'Azur.
|
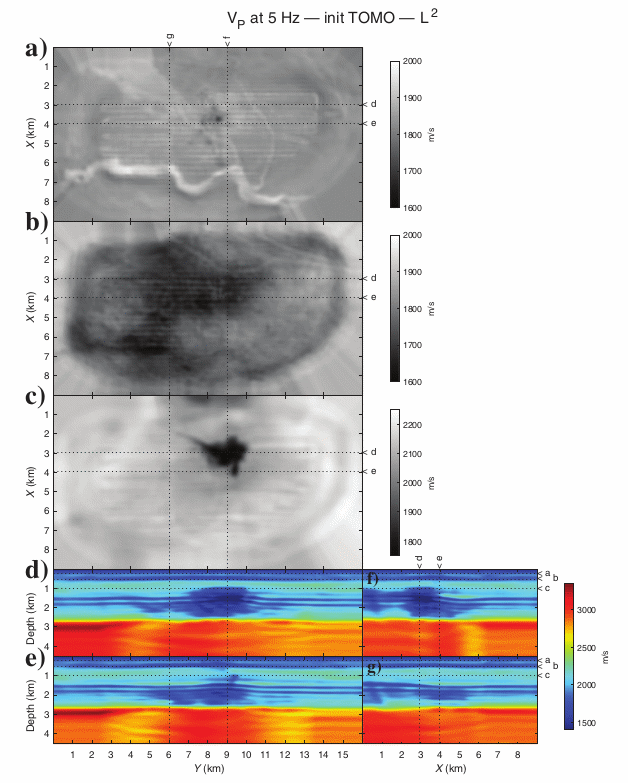
Slices of 3D FWI results from the Valhall field, from Pladys et al. 2022
2011-today |
Associate Professor in geophysics at Université Grenoble
Alpes |
2016 |
Habilitation (HDR) «Contributions to developments and applications of Full Waveform Modeling and Inversion » |
2010-2011 |
Post-Doc in Institut des Sciences de la Terre (previously Laboratoire de Geophysique Interne et Tectonophysique) at Université Joseph Fourier, Grenoble, France. "Multi-scale imaging by full waveform inversion" |
2006-2009 |
PhD Thesis in Géoazur Lab, University of Nice Sophia-Antipolis, France, under supervision of Jean Virieux and Stéphane Operto Seismic imaging of 2D visco-elastic media by full waveform inversion : methodological developements and applications |
2006 |
Research Master Degree (DEA) in Mechanical and Civil Engineering, Université de Bourgogne (France). Mention "très bien" (rang 1/7) |
2001-2006 |
Mechanical Engineer Degree from Institut Supérieur de l’Automobile et des Transports, Nevers (France).(major of promotion, rang 1/91) |
FWI : You can find here our open-source 2D frequency-domain visco-acoustic full waveform inversion code. This code can be used for your research and has been developed in the frame of the SEISCOPE project
Optimization : You can find here our open-source Optimization Tool box
In the frame of the SEISCOPE project, we also develop many other codes, not freely available.
If you are a company, you can be interested to support the SEISCOPE project
if you are academic and interested for collaboration, do not hesitate to contact me.
last update 07/2023
